参考

常见数据结构和 Javascript 实现总结
树的高度和深度以及结点的高度和深度

队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
let Queue = function () {
  // data 是存储元素的数组
  this.data = [];
};

// 入队
Queue.prototype.enqueue = function (element) {
  this.data.push(element);
};

// 出队
Queue.prototype.dequeue = function () {
  return this.data.splice(0, 1);
};

// 队列长度
Queue.prototype.length = function () {
  return this.data.length;
};

// 清空队列
Queue.prototype.empty = function () {
  this.data = [];
};

// 测试
// let q = new Queue()
// q.enqueue(1)
// q.enqueue(2)
// q.enqueue(3)
// log('length', q.length())
// log(q.dequeue())
// q.enqueue(4)
// log(q.dequeue())
// log(q.dequeue())
// log(q.dequeue())

栈 Stack

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
// 常见的 3 个操作：push pop top
let Stack = function() {
    this.data = []

// push 添加一个元素
Stack.prototype.push = function(e) {
    this.data.push(e)
}

// pop 删除并返回最新添加的元素
Stack.prototype.pop = function() {
    let index = this.data.length - 1
    return this.data.splice(index, 1)
}

// top 仅返回最新添加的元素
Stack.prototype.top = function() {
    let index = this.data.length - 1
    return this.data[index]
}

// test
/*
let s = new Stack()
s.push('hello')
s.push('world')
log(s.pop())
log(s.pop())

let str = 'hello'
for (let i = 0; i < str.length; i++) {
    s.push(str[i])
}

let str1 = ''
for (let i = 0; i < str.length; i++) {
    str1 += s.pop(str[i])
}
log(str1)
*/

链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
// 链表实现
let Node = function (e) {
  this.element = e;
  this.next = null;
};

// test
/*
let n1 = new Node(1)
let n2 = new Node(2)
let n3 = new Node(3)
n1.next = n2
n2.next = n3

let n = n1
while(n != null) {
    log('遍历链表', n.element)
    n = n.next
}
*/

let LinkedList = function () {
  this.head = new Node();
  this._length = 0;
};

// 在链表末尾 增加一个元素
LinkedList.prototype.append = function (e) {
  let node = new Node(e);
  let n = this.head;
  while (n.next != null) {
    n = n.next;
  }
  n.next = node;
  //
  this._length++;
};

// 返回一个元素的 index
LinkedList.prototype.indexOf = function (e) {
  let index = -1;
  let n = this.head;
  let i = 0;
  while (n.next != null) {
    if (e === n.element) {
      index = i;
      break;
    }
    n = n.next;
    i++;
  }
  return index;
};

// 返回链表的长度
LinkedList.prototype.length = function () {
  return this._length;
};

LinkedList.prototype.log = function () {
  let n = this.head.next;
  log("遍历链表");
  while (n != null) {
    log(" > ", n.element);
    n = n.next;
  }
};

// test
/*
let list = new LinkedList()
list.append('hello')
list.append('gua')
list.append('你好')
list.log()
log(list.length())
*/

其他数据结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/*
hash table  哈希表（散列表）
tree        树
set         集合
graph       图


哈希表就是用 字符串 当下标，也就是 js 中的对象的实现方式
也就是其他语言中的 字典

原理是用字符串 算出一个数字 然后用这个数字当下标存东西
比如 gua 这个字符串 我们用每个字符乘以一个数字最后求余得到下标
从字符串到数字的操作叫做 hash
// hash('gua') = 1
// hash('hs') = 3
【坑1， 坑2， 坑3， 坑4， 坑5， 坑6】
  gua       hs              wh
  xiao      lj
            bl



树一般是用来实现二叉搜索树的，应用范围不多
     6
    / \
   4   8
    \ / \
    57  9
    
*/

集合 Set

Set 中的元素 不重复、无序

常见方法

  • values： 返回集合中的所有元素
  • size： 返回集合中元素的个数
  • has： 判断集合中是否存在某个元素
  • add： 向集合中添加元素
  • remove： 从集合中移除某个元素
  • union： 返回两个集合的并集
  • intersection： 返回两个集合的交集
  • difference： 返回两个集合的差集
  • subset： 判断一个集合是否为另一个集合的子集
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
function MySet() {
  let collection = [];
  this.has = function (element) {
    // 如果不存在，则返回-1
    return collection.indexOf(element) !== -1;
  };

  this.values = function () {
    return collection;
  };

  this.size = function () {
    return collection.length;
  };

  this.add = function (element) {
    if (!this.has(element)) {
      collection.push(element);
      return true;
    }
    return false;
  };

  this.remove = function (element) {
    if (this.has(element)) {
      index = collection.indexOf(element);
      collection.splice(index, 1);
      return true;
    }
    return false;
  };

  this.union = function (otherSet) {
    let unionSet = new MySet();
    let firstSet = this.values();
    let secondSet = otherSet.values();
    firstSet.forEach(function (e) {
      unionSet.add(e);
    });
    secondSet.forEach(function (e) {
      unionSet.add(e);
    });
    return unionSet;
  };

  this.intersection = function (otherSet) {
    let intersectionSet = new MySet();
    let firstSet = this.values();
    firstSet.forEach(function (e) {
      if (otherSet.has(e)) {
        intersectionSet.add(e);
      }
    });
    return intersectionSet;
  };

  this.difference = function (otherSet) {
    let differenceSet = new MySet();
    let firstSet = this.values();
    firstSet.forEach(function (e) {
      if (!otherSet.has(e)) {
        differenceSet.add(e);
      }
    });
    return differenceSet;
  };

  this.subset = function (otherSet) {
    let firstSet = this.values();
    return firstSet.every(function (value) {
      return otherSet.has(value);
    });
  };
}

哈希表 Hash Table

Hash Table 内部使用一个 hash 函数将传入的键转换成一串数字，而这串数字将作为键值对实际的 key

常见方法

  • add： 增加一组键值对
  • remove： 删除一组键值对
  • lookup： 查找一个键对应的值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
function hash(string, max) {
  let hash = 0;
  for (let i = 0; i < string.length; i++) {
    hash += string.charCodeAt(i);
  }
  return hash % max;
}

function HashTable() {
  let storage = [];
  const storageLimit = 4;

  this.add = function (key, value) {
    let index = hash(key, storageLimit);
    if (storage[index] === undefined) {
      storage[index] = [[key, value]];
    } else {
      let inserted = false;
      for (let i = 0; i < storage[index].length; i++) {
        if (storage[index][i][0] === key) {
          storage[index][i][1] = value;
          inserted = true;
        }
      }
      if (inserted === false) {
        storage[index].push([key, value]);
      }
    }
  };

  this.remove = function (key) {
    let index = hash(key, storageLimit);
    if (storage[index].length === 1 && storage[index][0][0] === key) {
      delete storage[index];
    } else {
      for (let i = 0; i < storage[index]; i++) {
        if (storage[index][i][0] === key) {
          delete storage[index][i];
        }
      }
    }
  };

  this.lookup = function (key) {
    let index = hash(key, storageLimit);
    if (storage[index] === undefined) {
      return undefined;
    } else {
      for (let i = 0; i < storage[index].length; i++) {
        if (storage[index][i][0] === key) {
          return storage[index][i][1];
        }
      }
    }
  };
}

树

相关概念

  • Leaf（叶节点）：没有子节点的节点
  • Edge（边）：两个节点之间的连接线
  • Path（路径）：从源节点到目标节点的连续边
  • Degree of Node（节点的度）：表示拥有的子节点的个数
  • Height of Tree（树的高度）：也即深度，即树的最大层数（根节点层数从 1 开始，从 0 需减 1 层）
  • Height of Node（节点的高度）：该节点树内的叶节点的最大层数。叶节点高度为 1，往上节点的高度递增。一个节点的高度取最大值
  • Depth of Node（节点的深度）：从根节点到该节点的层数

层数一般从1开始

树节点的高度

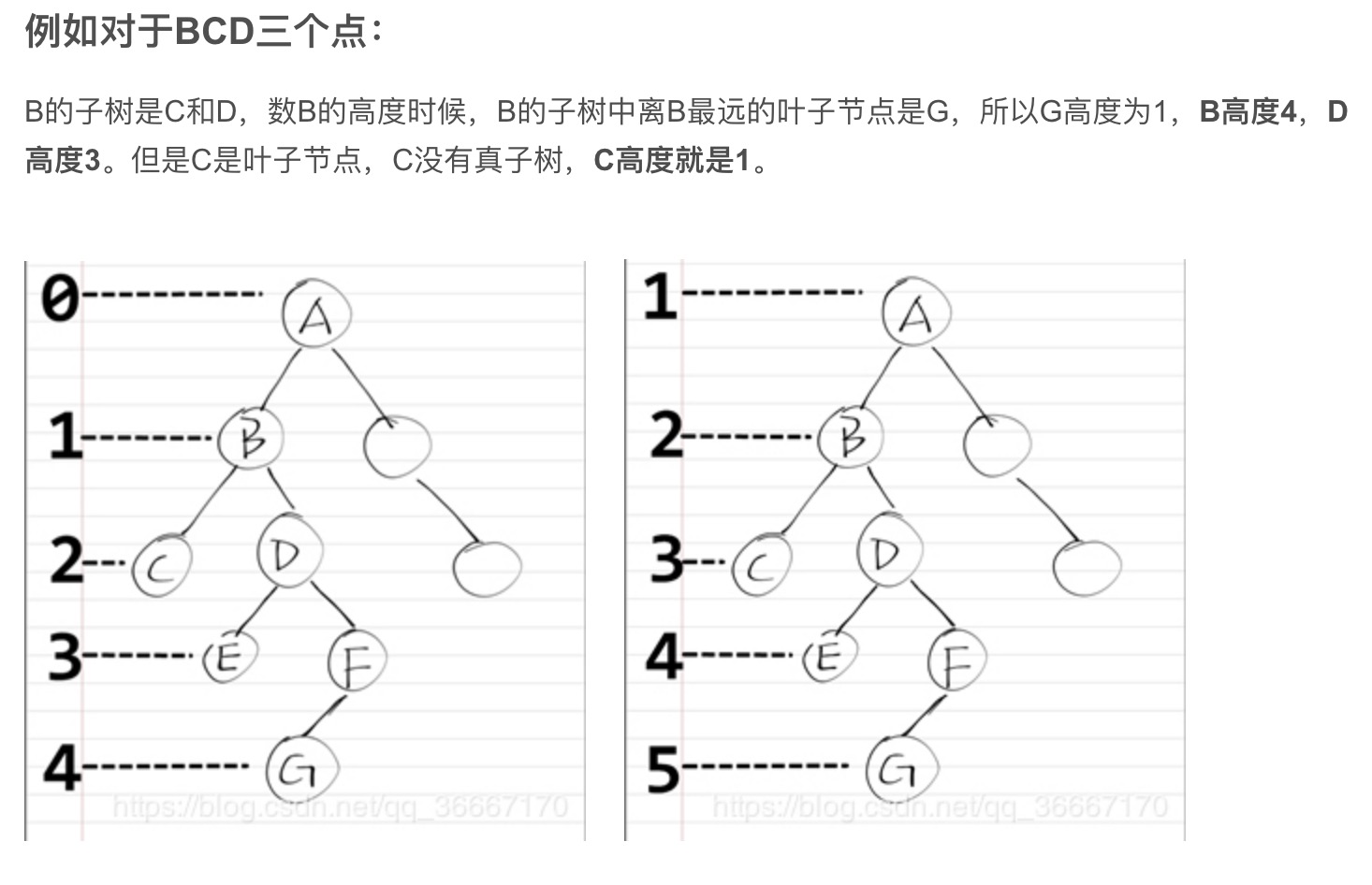
二叉查找树

每个节点最多只有两个子节点
左侧子节点 < 当前节点
右侧子节点 > 当前节点

常用方法

  • add：向树中插入一个节点
  • findMin：查找树中最小的节点
  • findMax：查找树中最大的节点
  • find：查找树中的某个节点
  • isPresent：判断某个节点在树中是否存在
  • remove：移除树中的某个节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
class Node {
  constructor(data, left = null, right = null) {
    this.data = data;
    this.left = left;
    this.right = right;
  }
}

class BST {
  constructor() {
    this.root = null;
  }

  add(data) {
    const node = this.root;
    if (node === null) {
      this.root = new Node(data);
      return;
    } else {
      const searchTree = function (node) {
        if (data < node.data) {
          if (node.left === null) {
            node.left = new Node(data);
            return;
          } else if (node.left !== null) {
            return searchTree(node.left);
          }
        } else if (data > node.data) {
          if (node.right === null) {
            node.right = new Node(data);
            return;
          } else if (node.right !== null) {
            return searchTree(node.right);
          }
        } else {
          return null;
        }
      };
      return searchTree(node);
    }
  }

  findMin() {
    let current = this.root;
    while (current.left !== null) {
      current = current.left;
    }
    return current.data;
  }

  findMax() {
    let current = this.root;
    while (current.right !== null) {
      current = current.right;
    }
    return current.data;
  }

  find(data) {
    let current = this.root;
    while (current.data !== data) {
      if (data < current.data) {
        current = current.left;
      } else {
        current = current.right;
      }
      if (current === null) {
        return null;
      }
    }
    return current;
  }

  isPresent(data) {
    let current = this.root;
    while (current) {
      if (data === current.data) {
        return true;
      }
      if (data < current.data) {
        current = current.left;
      } else {
        current = current.right;
      }
    }
    return false;
  }

  remove(data) {
    const removeNode = function (node, data) {
      if (node == null) {
        return null;
      }
      if (data == node.data) {
        // node没有子节点
        if (node.left == null && node.right == null) {
          return null;
        }
        // node没有左侧子节点
        if (node.left == null) {
          return node.right;
        }
        // node没有右侧子节点
        if (node.right == null) {
          return node.left;
        }
        // node有两个子节点
        var tempNode = node.right;
        while (tempNode.left !== null) {
          tempNode = tempNode.left;
        }
        node.data = tempNode.data;
        node.right = removeNode(node.right, tempNode.data);
        return node;
      } else if (data < node.data) {
        node.left = removeNode(node.left, data);
        return node;
      } else {
        node.right = removeNode(node.right, data);
        return node;
      }
    };
    this.root = removeNode(this.root, data);
  }
}

// 测试
const bst = new BST();
bst.add(4);
bst.add(2);
bst.add(6);
bst.add(1);
bst.add(3);
bst.add(5);
bst.add(7);
bst.remove(4);
console.log(bst.findMin());
console.log(bst.findMax());
bst.remove(7);
console.log(bst.findMax());
console.log(bst.isPresent(4));

字典树 Trie

Trie 也可以叫做 Prefix Tree（前缀树），也是一种搜索树。

Trie分步骤存储数据，树中的每个节点代表一个步骤，trie 常用于

存储单词以便快速查找，比如实现单词的自动完成功能。

Trie 中的每个节点都包含一个单词的字母，跟着树的分支可以可以拼写出

一个完整的单词，每个节点还包含一个布尔值表示该节点是否是单词的最后一个字母

常用方法

  • add：向字典树中增加一个单词
  • isWord：判断字典树中是否包含某个单词
  • print：返回字典树中的所有单词
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
/**
 * Trie的节点
 */
function Node() {
  this.keys = new Map();
  this.end = false;
  this.setEnd = function () {
    this.end = true;
  };
  this.isEnd = function () {
    return this.end;
  };
}

function Trie() {
  this.root = new Node();

  this.add = function (input, node = this.root) {
    if (input.length === 0) {
      node.setEnd();
      return;
    } else if (!node.keys.has(input[0])) {
      node.keys.set(input[0], new Node());
      return this.add(input.substr(1), node.keys.get(input[0]));
    } else {
      return this.add(input.substr(1), node.keys.get(input[0]));
    }
  };

  this.isWord = function (word) {
    let node = this.root;
    while (word.length > 1) {
      if (!node.keys.has(word[0])) {
        return false;
      } else {
        node = node.keys.get(word[0]);
        word = word.substr(1);
      }
    }
    return node.keys.has(word) && node.keys.get(word).isEnd() ? true : false;
  };

  this.print = function () {
    let words = new Array();
    let search = function (node = this.root, string) {
      if (node.keys.size != 0) {
        for (let letter of node.keys.keys()) {
          search(node.keys.get(letter), string.concat(letter));
        }
        if (node.isEnd()) {
          words.push(string);
        }
      } else {
        string.length > 0 ? words.push(string) : undefined;
        return;
      }
    };
    search(this.root, new String());
    return words.length > 0 ? words : null;
  };
}

图 Graph

分 有向图 和 无向图

js 中常用矩阵表示

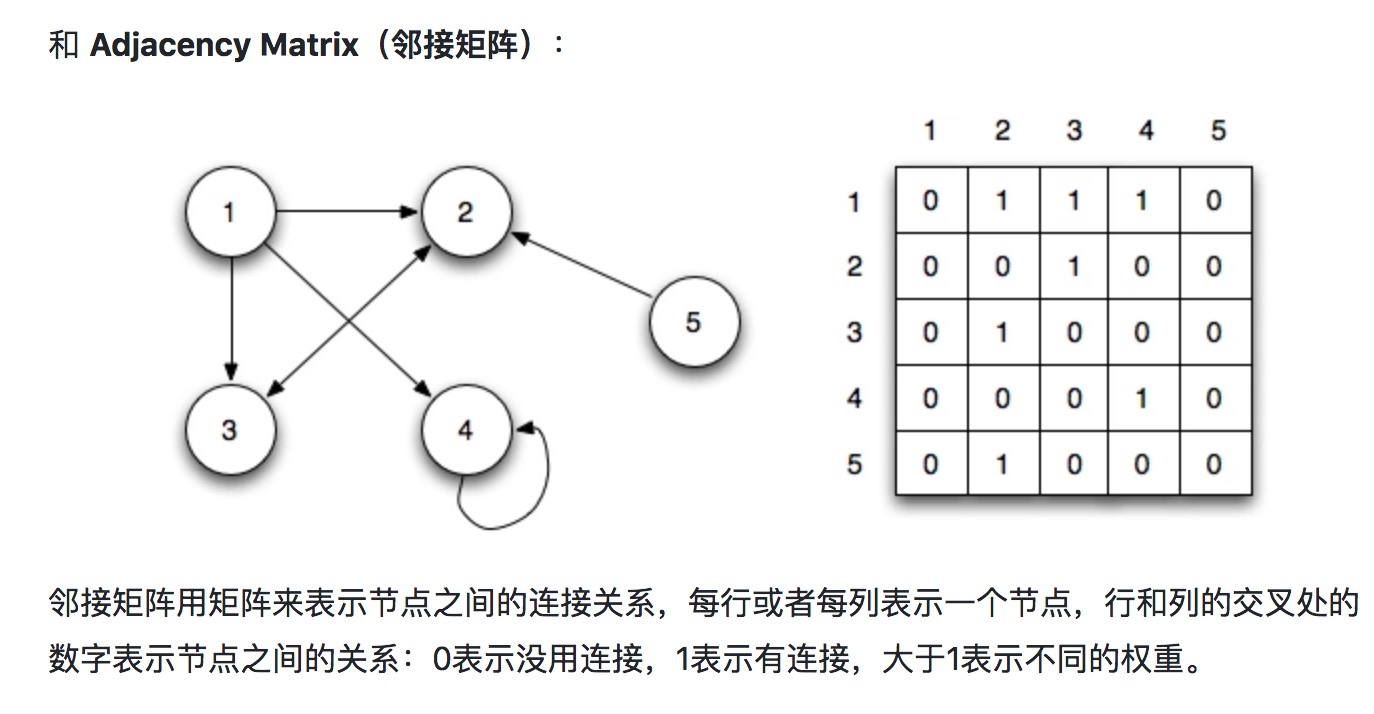
连接：节点 A 箭头朝外指向其他节点 B，称 A 连接 B

广度优先搜索算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
function bfs(graph, root) {
  var nodesLen = {};

  for (var i = 0; i < graph.length; i++) {
    nodesLen[i] = Infinity;
  }

  nodesLen[root] = 0;

  var queue = [root];
  var current;

  while (queue.length != 0) {
    current = queue.shift();

    var curConnected = graph[current];
    var neighborIdx = [];
    var idx = curConnected.indexOf(1);
    while (idx != -1) {
      neighborIdx.push(idx);
      idx = curConnected.indexOf(1, idx + 1);
    }

    for (var j = 0; j < neighborIdx.length; j++) {
      if (nodesLen[neighborIdx[j]] == Infinity) {
        nodesLen[neighborIdx[j]] = nodesLen[current] + 1;
        queue.push(neighborIdx[j]);
      }
    }
  }

  return nodesLen;
}

// 测试
var graph = [
  [0, 1, 1, 1, 0],
  [0, 0, 1, 0, 0],
  [1, 1, 0, 0, 0],
  [0, 0, 0, 1, 0],
  [0, 1, 0, 0, 0],
];

console.log(bfs(graph, 1));
// {
//   0: 2,
//   1: 0,
//   2: 1,
//   3: 3,
//   4: Infinity
// }